Making Sense of Quantum Mechanics
Do electrons decide to behave like particles only when someone looks at them? When exactly does a wavefunction 'collapse'?
With QM being introduced to the public via memes about the Schrodinger’s cat and movies like Ant-man slapping the adjective “quantum” to cover every plot hole, there are a lot of misconceptions out there that make QM look like a religion.

These misconceptions primarily come from:
- Over-simplifying concepts to the point they are actually completely wrong (Feynman warned against this)
- Misunderstanding the meaning of well-defined terms such as “observation/measurement” to be “a guy looking at them”.
- Trying to interpret QM in a classical way, without leaving our comfort zone.
I had a long discussion with my good friend Kasun Withana on these topics, and I decided to sum them up here, to help build a frame of mind where QM makes sense.
The Wavefunction
Let’s start with the true nature of particles. Particles are stuff that is each governed by a fundamental 'wavefunction'. The wavefunction is THE most fundamental thing. It's not just another property of a particle. It's THE particle.
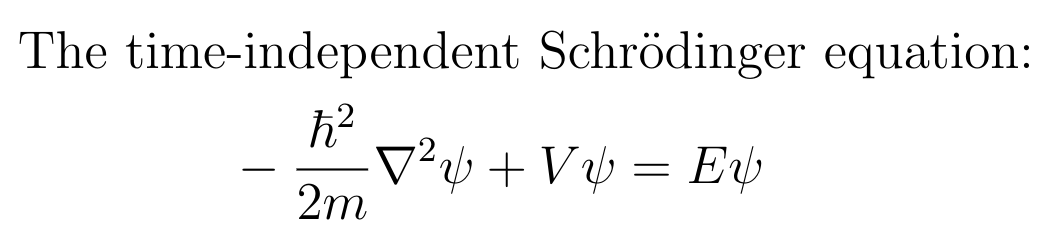
The wavefunction(s) of a particle is defined as the solution(s) to Schrodinger’s complex-valued wave equation, constrained by the potential field.
Fun fact: the time-independent Schrodinger’s Equation is just a simple harmonic equation. Called harmonic oscillators, the simple harmonic equation of the following form is surprisingly common in the foundations of different branches of physics. The following video explains why, in an approachable way.
\[ \ddot{x} = -k x \]
Observables
We cannot measure the wavefunction directly. It's always behind the scenes. We can only measure the 'observables'. Properties of the given particle such as momentum, position... are called observables and are all just different 'views' or projections of this wavefunction. We get the position 'distribution' of the particle by applying the position 'operator' on the wavefunction.
Distribution? Yes. These observables (position, momentum) are not numbers. Each of them is a probability distribution over all its possible values. We need to wrap our heads around the fact that the nature of reality is probabilistic on the most fundamental level.
It’s not like we are unable to build a device to measure a particle’s position. The particle actually doesn’t have a 'position'.
Operators
A mathematical operator maps/projects one function space into another. Differentiation is an operator, Fourier transform is another. Both are linear operators. Operators are functions that operate on functions.
The probability distribution of the observables (position, momentum) of a particle are the projections of the underlying wavefunction through a respective linear operator (listed below). Note that the wavefunction itself is unitless, but the projected function resulting from an operator has the units of the operator itself.

Heisenberg's Uncertainty Principle
Here comes the fun part. Position and momentum operators are Fourier transform pairs of each other. Just like time and frequency.
A quick recap on the Fourier domain. Time and Frequency are Fourier transform pairs. In a given song, if you want to find where (time) a specific frequency comes up, you cut the song into tiny intervals and take the Short Term Fourier Transform. Then we would lose the precision on frequency. In a spectrogram (frequency-time plot of a song), as you finely sample the time axis, the frequency axis gets fuzzier. And vice versa. It is impossible to find both frequency and the time where it occurs with high accuracy.
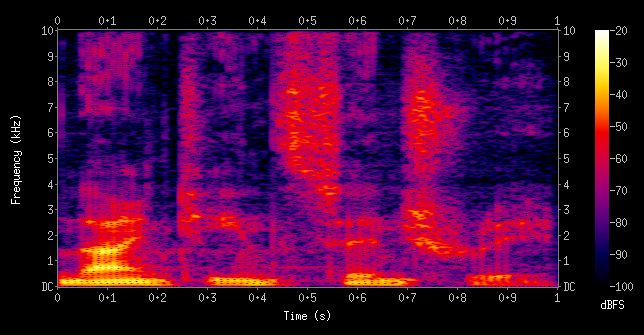
The same thing happens with position and momentum, which are Fourier pairs. Firstly, we cannot measure/observe a property of a particle, without interacting with the particle. When two particles interact, their wavefunctions interact and modify each other. If we set up a detector to 'read' the position, that is if we set up stuff that interacts with the wavefunction to make its position distribution sharper, the momentum distribution automatically becomes fuzzier.
\[ \Delta x \cdot \Delta p \geq \dfrac{h}{4 \pi}\]
Heisenberg’s uncertainty principle follows this. The product of the error in position measurement (Δx) and momentum measurement (Δp) is always bigger than a known constant. Because the position and momentum don’t exist for a particle with arbitrary accuracy. This is the mathematical nature of reality. Comes from the fact that those operators are a Fourier transform pair.
Ok, from this we can look at wavefunction collapse.
Wavefunction Collapse
Wavefunction never 'collapses'. Say, we set up a detector to read position. That detector does it by interacting with the particle, modifying its wavefunction to make the position distribution 'view' sharper (uncertainty in that 'view' is reduced). That will never be 100% sharp as a point. This means we can never know the exact location of the particle. Because it doesn't actually have a position.
This is what we call 'it behaves as a particle'. In reality, it doesn't behave as anything. It is what it is. The wavefunction has not 'collapsed'. Instead, by making one 'view' of the wavefunction sharper, we have made the other view (momentum) fuzzier. The wavefunction is still there its full majestic form. If that particle goes on to interact with another detector that now tries to measure momentum (modify the wavefunction to make momentum 'view' sharper), the position gets fuzzier.
This is what happens in the double-slit experiment as well. Since it is an experiment focused on reading the position 'view', we don't talk about momentum. This is why we loosely say things like “wavefunction collapses at the detector” and “electron behaves as a particle when measured”. However, in our attempt at trying to read the position by making position 'view' sharper (more particle-like), we have just made the momentum 'view' of the same particle fuzzier (more wave-like).
Isn't it fascinating to know that 'imaginary' numbers and Fourier transform are at the foundations of reality itself?
My exposure to hardcore QM is a basic module and an assignment on numerically solving the Schrodinger equation in 1D, 2D, and 3D. It was fun to see how the atomic orbitals are just simple harmonic motion in space in 3D. If anyone finds a mistake in this write-up, feel free to point it out.
First posted on Facebook:

Example: Solving the Schrodinger Equation

When you put an electron in a 1D space, within two barriers of voltage (potential well), and you want to find the position of the electron. Interestingly, the electron doesn't have a position, but only has a probability distribution over space, which is found by solving the Schrodinger Equation in 1D.
That distribution is a set of 1D waves in space, the fundamental frequency, first overtone, second overtone...etc based on the gap between two barriers, as shown above. If the electron is given the energy 0.03 eV, it will be like the bottom one (fundamental frequency). The electron will have a higher probability of existence at the center.
If it's given energy of about 0.5 eV, it will have the probability distribution that looks like the first overtone. That is, there is very little probability of the electron existing at the center.
Note how the electron can only take discrete energy values. You can't just give 0.25 eV of energy. The electron will not accept that. So, we say energy is "quantized". That gives the name quantum mechanics.
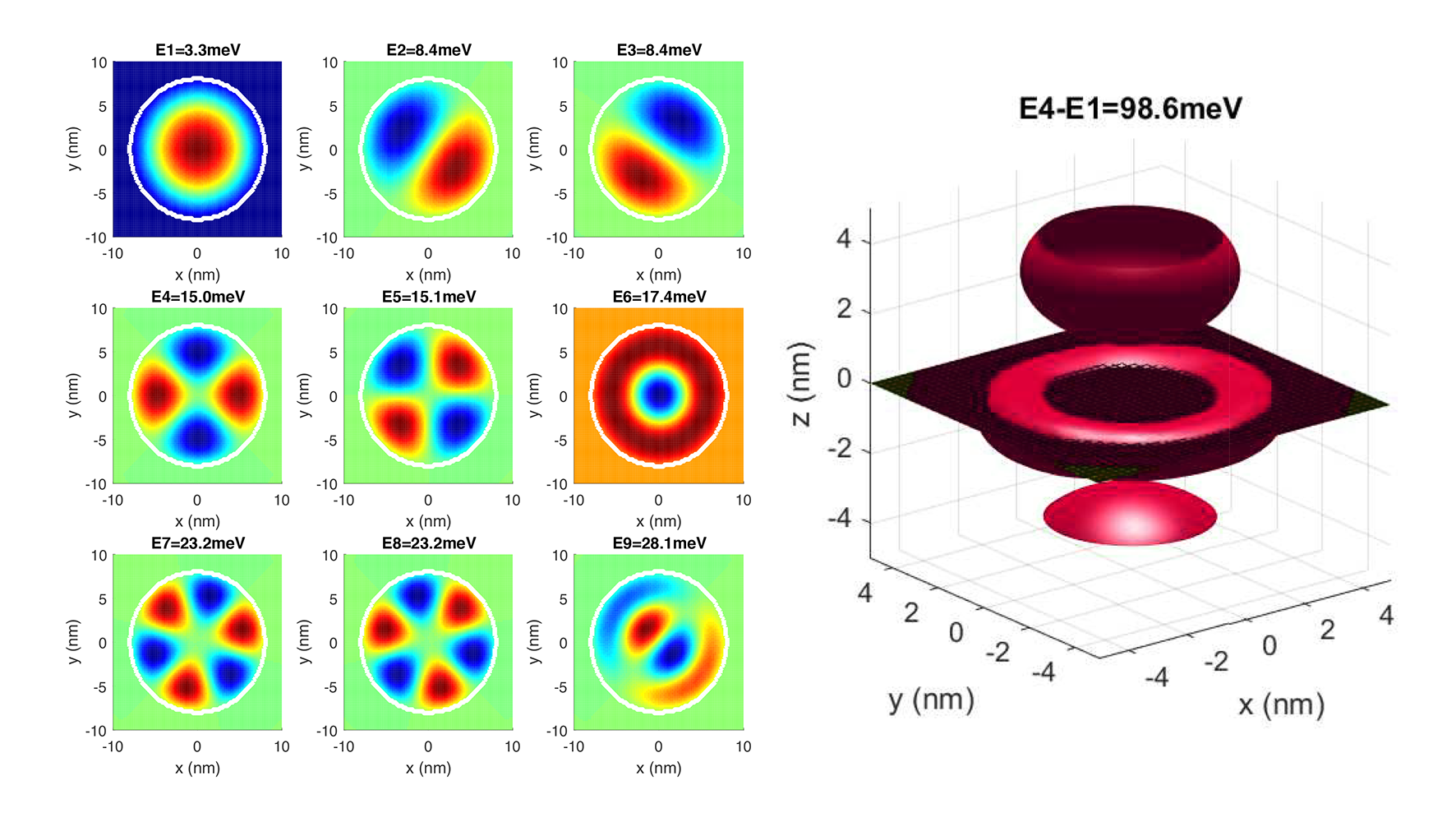
Generalizing for any case, if you know the potential (voltage) field of the space, charge, and mass of the particle, you can find a function called the Hamiltonian. Its eigenvalues are the possible values of energy that the electron can take. Its corresponding eigenfunctions are the wavefunctions of the particle. The norm square of the wavefunction will be the probability.
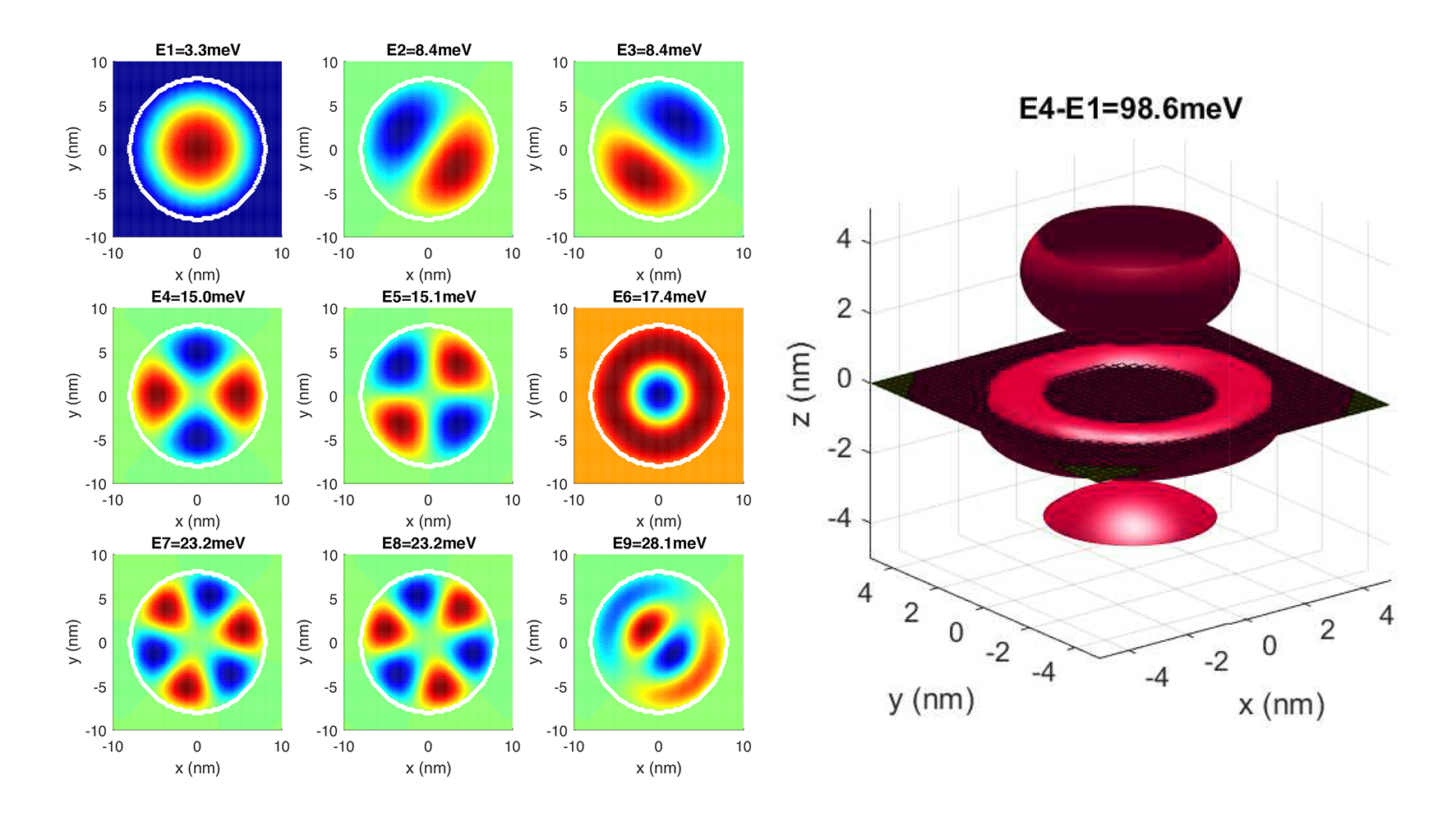
When you solve this numerically (when you cut the space into a grid), everything become matrices. Potential becomes a matrix (each value corresponds to that value in space). Then wavefunctions are eigenvectors. This way, we can easily solve the static (time-independent Schrodinger equation) easily for 2D (left) and 3D (right) as well. When you solve it for the potential field of a proton, you get the s-p-d orbitals of a hydrogen atom as shown. See the following post for the math and code.
Quantum Tunneling
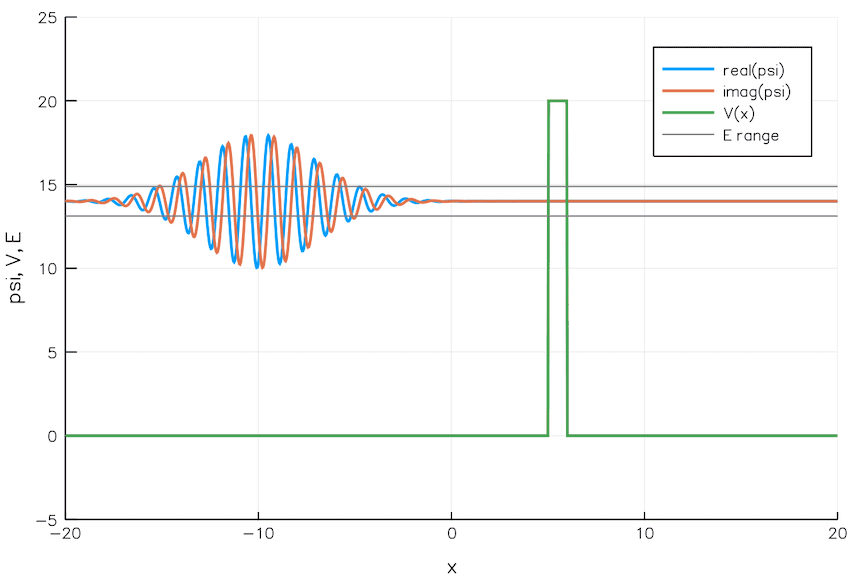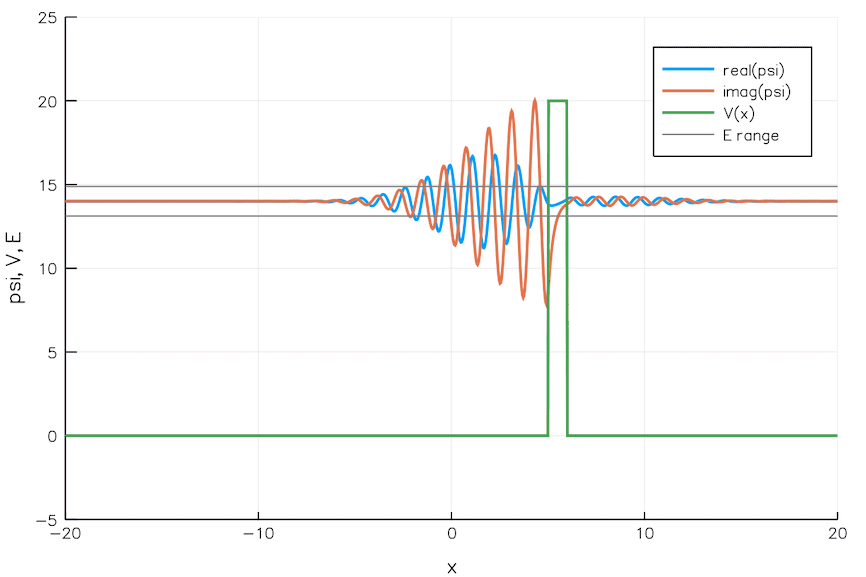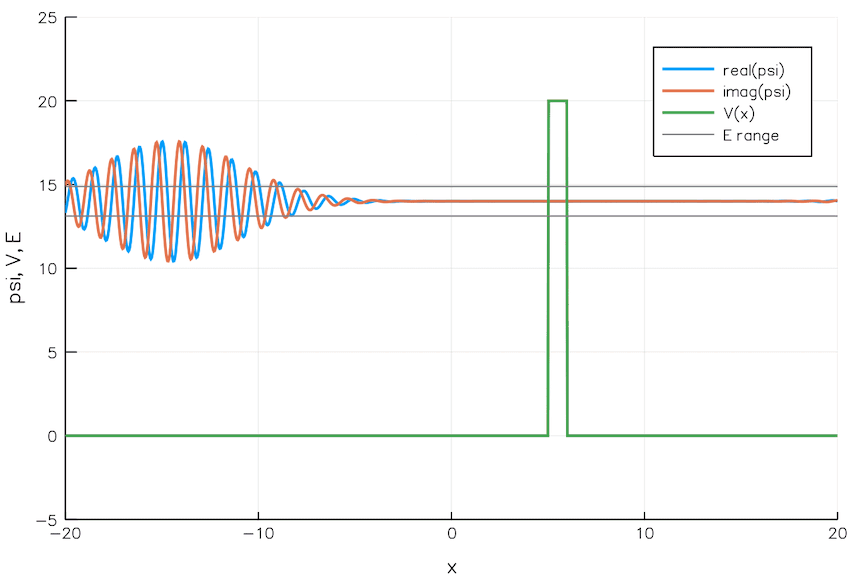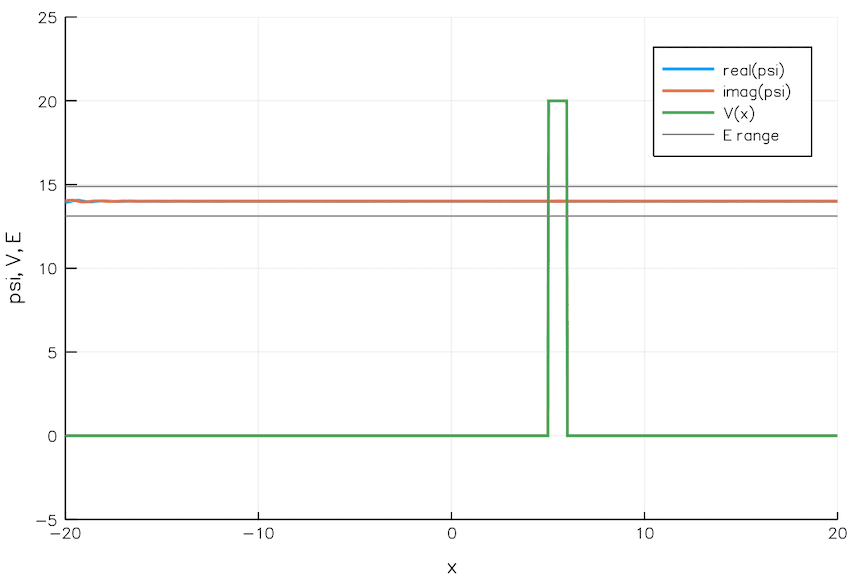
We currently build chips with transistors 5 nm wide. That is the width of 24 Si atoms. As we go smaller and smaller, the quantum mechanical effects pose significant problems. For example, electrons can leak through a switched-off transistor (voltage barrier) via quantum tunneling, wreaking havoc.
Alternative Derivation of QM
To add to the post, Quantum Mechanics can also be seen this way. Probability theory is when the sum of probabilities of being in each state adds up to one. That is, the L1 norm of the state-probability vector is 1. What if we set the L2 norm of that vector to 1? Then you get Quantum Mechanics!!
In this article, the author derives QM mathematically, as a natural generalization of probabilities when we allow them to take negative and complex values. He explains why the wavefunction is complex-valued and why only L1 and L2 norms make sense for probabilities and so on...
"Quantum mechanics is what you would inevitably come up with if you started from probability theory and then said, let's try to generalize it so that the numbers we used to call "probabilities" can be negative numbers. As such, the theory could have been invented by mathematicians in the 19th century without any input from experiments. It wasn't, but it could have been."
Okay, I'm a layman, where do I start?
The following MIT lecture serves as a good, formal introduction to quantum mechanics. It is captivating and easily understandable, without much prior knowledge. The highly enthusiastic lecturer goes through the following facts and experimental evidence that gave birth to quantum mechanics:
- Atoms Exist
- Randomness Exists
- Atomic Spectra: discrete & structural
- Photoelectric Effect
- Electron Diffraction
- Bell's Inequality





