Aba's Blog

Solving Schrödinger's Equation in 1,2,3-D with MATLAB

Technical Projects Feb 19, 2019

In my junior year, I picked an elective on Quantum Mechanics: Electronic Devices. The project that was worth 50% was to solve the time-independent Schrodinger's equation in 1,2,3-D numerically, using MATLAB.

I already had a fascination for modern physics. Therefore, I spent disproportionately more time on this project. I researched a lot, learned about numerical methods and the intuition of Schrodinger's Equation.

Through this, I understood Schrodinger's equation in two levels:

  1. Mathematically, it is a simple-harmonic-motion in space. I was fascinated to find that in 3-D, with a point charge, this SHM yields the s-p-d orbitals of the hydrogen atom. Later I found that such 'harmonic oscillators' are found at the foundations of different branches of physics.
  2. It basically says that wavefunctions are the eigenfunctions and the discrete energy values are the eigenvalues of the Hamiltonian operator, which is constrained by the potential field.

Although I learned eigen-things in Linear Algebra class, I did not have an intuition for them. Therefore, I spent a few days building up a deeper intuition about them. I watched this entire series, took copious notes.

I then started programming using some references. While we were asked only to do it for either 1,2 or 3D using any method, I went the extra mile and did it for all three, using two methods.

For better intuition on wavefunctions and observables of Quantum Mechanics, check out my following post:

Making Sense of Quantum Mechanics​
Do electrons decide to behave like particles only when someone looks at them? When exactly does a wavefunction ‘collapse’? ​With QM being introduced to the masses via memes of Schrodinger’s cat and with movies like Ant-man slapping the adjective “quantum” ​ on every plot hole, there are a lot of
Aba's BlogAbarajithan G

Report

The intuition I gained from this, led me to write this explanation of basic QM, and this rant about how Linear Algebra is introduced poorly.

MATLAB Code

Two of the five Matlab programs I wrote are given here for reference.

Solving 1D equation directly

clear all
close all
clc

% Parameters
n=4;
Nx = 200;
Lmax = 4e-8;

% Constants
h =6.626E-34;
hbar =h/(2*pi);
e =1.602E-19; 
me =9.109E-31;


% Potential
x = linspace(0,Lmax, Nx);
V = 0.3*[ones(1,50) zeros(1,100) ones(1,50)];
%V = 0.01*sin(1E11*pi*x);

%% Direct Method
dx=x(2)-x(1);

% Build Laplacian
DX2 = (-2)*diag(ones(1,Nx)) + (1)*diag(ones(1,Nx-1),-1) + (1)*diag(ones(1,Nx-1),1);
DX2 = DX2/dx^2;

% Build Hamiltonian
H = -hbar^2/(2*me) * DX2  +  diag(V*e);

% Solve for Eigenfunction
H = sparse(H);
[psi,Energy] = eigs(H,n,'SM');
E = diag(Energy)/e ;      %Divide by e for eV units
E = abs(E);

% Normalize Wavefunction
for i=1:n
    psi(:,i)=psi(:,i)/sqrt(trapz(x',abs(psi(:,i)).^2));
end

psi=psi(:,end:-1:1);
E=E(end:-1:1);

%% Plot Results

% Normalise for plotting
for i=1:length(E)
      psi(:,i)=abs(psi(:,i)).^2/max(abs(psi(:,i)).^2)*0.04 + E(i)*15;
end

LW=2;
figure
for i=1:length(E)
    
    plot(x*1e9,V, 'b-','linewidth',LW)
    hold on;
    plot(x*1e9,psi(:,i),'r-','linewidth',LW)
    
    xlabel('x (nm)');
    ylabel('Energy (eV)');

    ylim([min(V)-0.05 max(V)+0.1])
    hold on;
end
hold off;

Solving 3D equation in fourier domain

clear all
close all
clc

% Constants

h=6.62606896E-34;              
hbar=h/(2*pi);
e=1.602176487E-19;             
me=9.10938188E-31;
ep0 = 8.854E-12;

n=12;
Nx=64;                  
Ny=64;                  
Nz=64;

Mass = 0.23;            
Mx=15e-9;               
My=15e-9;               
Mz=4e-9;        

x=linspace(-Mx/2,Mx/2,Nx);
y=linspace(-My/2,My/2,Ny);
z=linspace(-Mz,Mz,Nz)+0.5e-9;

[X,Y,Z]=meshgrid(x,y,z);


%% Define Potential

% V=1.5;
% V0 = (1-index) * V; 
% 1. Rectangular potential well
%index = (X > -Mx*0.4) .* (X < Mx*0.4) .* (Y > -My*0.4) .* (Y < My*0.4).* (Z > -Mz*0.4) .* (Z < Mz*0.4);
% 2. Circular potential well
%index = (X.^2 + Y.^2 + Z.^2) < (Mx*0.4)^2;
% 3. Point charge - hydrogen atom
V0 = (1/(4*pi*ep0))*(1-e/(sqrt(X.^2+Y.^2+Z.^2)));

%% Fourier Method

Nx = 64 ;        
Ny = 64 ;        
Nz = 64 ;        
NGx = 15;
NGy = 13;
NGz = 11;

% Building the fourier space
NGx = 2*floor(NGx/2);          
NGy = 2*floor(NGy/2);          
NGz = 2*floor(NGz/2);          

[X,Y,Z] = meshgrid(x,y,z);
xx=linspace(x(1),x(end),Nx);
yy=linspace(y(1),y(end),Ny);
zz=linspace(z(1),z(end),Nz);
[XX,YY,ZZ] = meshgrid(xx,yy,zz);

V=interp3(X,Y,Z,V0,XX,YY,ZZ);

dx=x(2)-x(1);
dxx=xx(2)-xx(1);
dy=y(2)-y(1);
dyy=yy(2)-yy(1);
dz=z(2)-z(1);
dzz=zz(2)-zz(1);
Ltotx=xx(end)-xx(1);
Ltoty=yy(end)-yy(1);
Ltotz=zz(end)-zz(1);

[XX,YY,ZZ] = meshgrid(xx,yy,zz);

% Potential function in Fourier space
Vk = fftshift(fftn(V))*dxx*dyy*dzz/Ltotx/Ltoty/Ltotz;
Vk =Vk(Ny/2-NGy+1:Ny/2+NGy+1 , Nx/2-NGx+1:Nx/2+NGx+1 , Nz/2-NGz+1:Nz/2+NGz+1);

% k vectors
Gx = (-NGx/2:NGx/2)'*2*pi/Ltotx;
Gy = (-NGy/2:NGy/2)'*2*pi/Ltoty;
Gz = (-NGz/2:NGz/2)'*2*pi/Ltotz;

NGx=length(Gx);
NGy=length(Gy);
NGz=length(Gz);
NG=NGx*NGy*NGz;

% Building Hamiltonian 
idx_x = reshape(1:NGx, [1 NGx 1]);
idx_x = repmat(idx_x, [NGy 1 NGz]);
idx_x = idx_x(:);

idx_y = reshape(1:NGy, [NGy 1 1]);
idx_y = repmat(idx_y, [1 NGx NGz]);
idx_y = idx_y(:);

idx_z = reshape(1:NGz, [1 1 NGz]);
idx_z = repmat(idx_z, [NGy NGx 1]);
idx_z = idx_z(:);

idx_X = (repmat(idx_x,[1 NG])-repmat(idx_x',[NG 1])) + NGx;     
idx_Y = (repmat(idx_y,[1 NG])-repmat(idx_y',[NG 1])) + NGy;     
idx_Z = (repmat(idx_z,[1 NG])-repmat(idx_z',[NG 1])) + NGz;     

idx = sub2ind(size(Vk), idx_Y(:), idx_X(:), idx_Z(:));
idx = reshape(idx, [NG NG]);

GX = diag(Gx(idx_x));
GY = diag(Gy(idx_y));
GZ = diag(Gz(idx_z));

D2 = GX.^2 + GY.^2 + GZ.^2 ;

H =  hbar^2/(2*me*Mass)*D2  +  Vk(idx)*e ;

% Solving for eigs
H = sparse(H);
[psik, Ek] = eigs(H,n,'SM');
E = diag(Ek)  / e;
E=real(E);

% Invert and normalize wavefunctions
for j=1:n
    PSI = reshape(psik(:,j),[NGy,NGx,NGz]);
    
    % Inverse FT
    Nkx=length(PSI(1,:,1));
    Nky=length(PSI(:,1,1));
    Nkz=length(PSI(1,1,:));

    Nx1=Nx/2-floor(Nkx/2);
    Nx2=Nx/2+ceil(Nkx/2);
    Ny1=Ny/2-floor(Nky/2);
    Ny2=Ny/2+ceil(Nky/2);
    Nz1=Nz/2-floor(Nkz/2);
    Nz2=Nz/2+ceil(Nkz/2);

    PSI00=zeros(Ny,Nx,Nz);
    PSI00( Ny1+1:Ny2 , Nx1+1:Nx2 , Nz1+1:Nz2)=PSI;
    PSI=ifftn(ifftshift(PSI00));
    
    
    PSI = PSI/(dxx*dyy*dzz) ;
    psi_temp = interp3(XX,YY,ZZ,PSI,X,Y,Z);
    psi(:,:,:,j) = psi_temp / max(psi_temp(:));
end

%% Plot results

c=0;
ii=0;
for i=1:n
    if i>18
      break
    end
    if i==1 || i==5 || i==9 || i == 13
      figure
      c=c+1;
      ii=0;
    end
    ii=ii+1;
    
    subplot(2,2,ii,'fontsize',10)
    hold on;grid on;view (-38, 20);
    
    idz=find(z>0);idz=idz(1);
    pcolor(x*1e9,y*1e9,squeeze(V0(:,:,idz)))
    colormap(jet)
       
    PSI=abs(psi(:,:,:,i)).^2;
    
    p = patch(isosurface(x*1e9,y*1e9,z*1e9,PSI,max(PSI(:))/6));
    isonormals(x*1e9,y*1e9,z*1e9,PSI, p)
    set(p, 'FaceColor', 'blue', 'EdgeColor', 'none', 'FaceLighting', 'gouraud')
    daspect([1,1,1])
    light ('Position', [1 1 5]);
    M=max([Mx My]);
    xlim([-1 1]*M/3*1e9)
    ylim([-1 1]*M/3*1e9)
    zlim([-1 1]*M/3*1e9)
    
    xlabel('x (nm)')
    ylabel('y (nm)')
    zlabel('z (nm)')
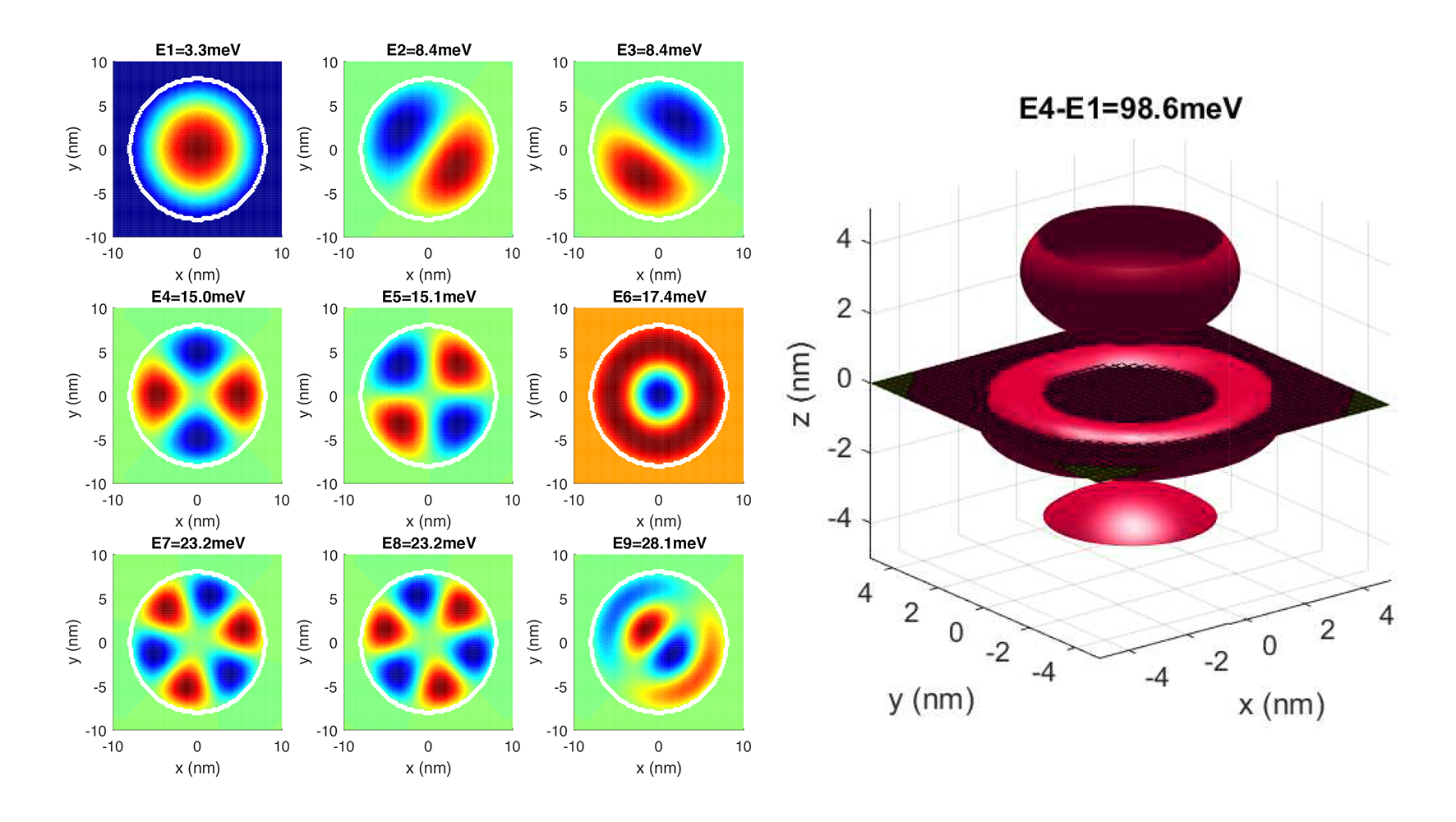
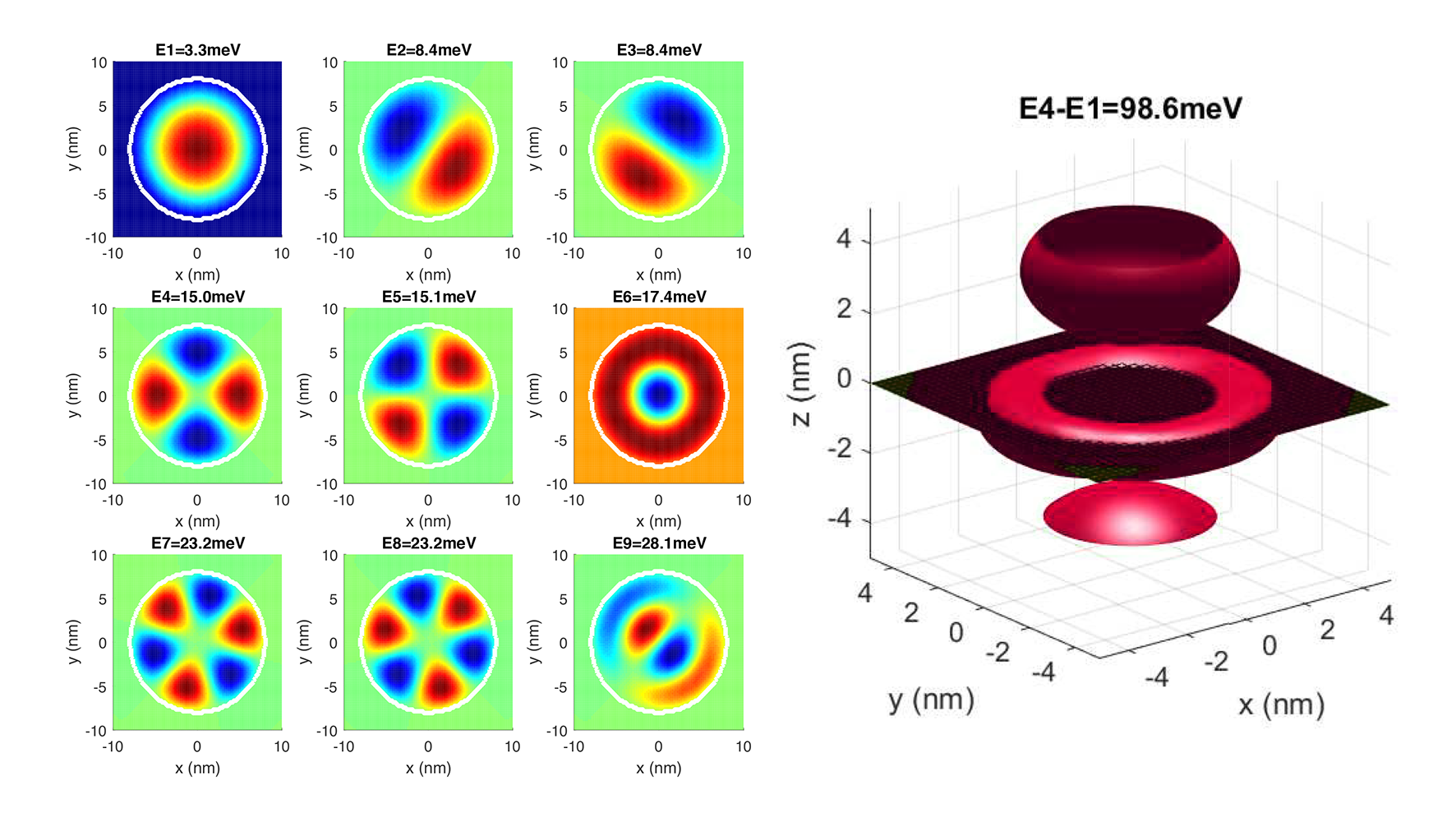
    title(strcat('E',num2str(i),'-E1=',num2str((E(i)-E(1))*1000,'%.1f'),'meV'))
end

References

  • [1] “(17) A Numerical Approach to the Solution of Schrodinger Equation for Hydrogen-Like Atoms | Request PDF,” ResearchGate. [Online]. Available: https://www.researchgate.net/publication/305818710_A_Numerical_Approach_to_the_Solution_of_Schrodinger_Equation_for_Hydrogen-Like_Atoms.
  • [2] LaurentNevou, 3D Time independent Schroedinger equation solver. Contribute to LaurentNevou/Q_Schrodinger3D_demo development by creating an account on GitHub. 2019.
  • [3] M. A. Mahmood, “A Numerical Approach to the Solution of Schrodinger Equation for Hydrogen-Like Atoms,” IOSR Journal of Dental and Medical Sciences, vol. 15, no. 07, pp. 128–131, Jul. 2016.
  • [5] S. P. Novikov, “Discrete Schrodinger operators and topology,” arXiv:math-ph/9903025, Mar. 1999.
  • [6] I. Cooper, “DOING PHYSICS WITH MATLAB QUANTUM PHYSICS HYDROGEN ATOM HYDROGEN-LIKE IONS,” p. 40.
  • [7] I. Cooper, “DOING PHYSICS WITH MATLAB QUANTUM PHYSICS SCHRODINGER EQUATION,” p. 7.
  • [9] “Fourier Transforms of the Time Independent Schroedinger Equation.” [Online]. Available: http://www.sjsu.edu/faculty/watkins/schrofourier.htm.
  • [10] “Generate sparse matrix for the Laplacian differential operator ∇2u for 3D grid.” [Online]. Available: https://www.12000.org/my_notes/mma_matlab_control/KERNEL/KEse83.htm
  • [12] “LAPLACIAN - The Discrete Laplacian Operator.” [Online]. Available: https://people.sc.fsu.edu/~jburkardt/m_src/laplacian/laplacian.html.
  • [13] M. A. Mahmood, “Novel Numerical Solution of Schrodinger Equation for Hydrogen-like Atoms,” vol. 6, no. 3, p. 5, 2015.
  • [14] G. Lindblad, “Quantum Mechanics with MATLAB,” p. 28.

Tags

Recommended for you